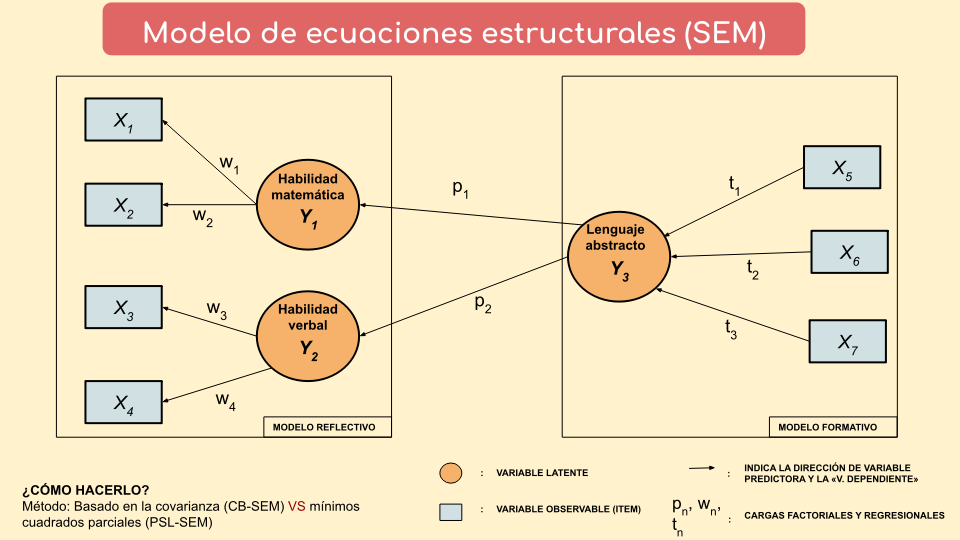
Los modelos de ecuaciones estructurales (SEM) son un conjunto de técnicas estadísticas multivariadas, denominadas de segunda generación, que combinan el uso del análisis factorial y la regresión. De esta manera, se puede experimentar a través de modelos estadísticos, fundamentados teóricamente, aspectos más amplios del comportamiento humano. Los SEM han sido difundidos cada vez más en los últimos años, buscando superar las debilidades que tenían las técnicas multivariadas de primera generación (por ejemplo, análisis clúster, análisis de varianza o regresión múltiple). En este sentido, los SEM permiten la incorporación de variables latentes o no observables medidas por variables observables o indicadores.

Dentro de los SEM existen dos tipos o aproximaciones, la basada en la covarianza (CB-SEM) y otra basada en la varianza o de método de mínimos cuadrados parciales (PLS-SEM). En esta oportunidad, nos centraremos en esta segunda técnica. El PLS-SEM estima coeficientes que maximizan la varianza explicada de los constructos endógenos (variables dependientes), otorgando la característica predictora a esta técnica estadística. Entre las ventajas que tiene el PLS-SEM (Hair et al., 2011) es que, (a) no presenta problemas de identificación con tamaños muestrales reducidos, alcanzando usualmente altos niveles de potencia estadística con pequeños tamaños muestrales; (b) no tiene supuestos respecto a la distribución de los datos dado que es un método no paramétrico; (c) es robusto ante la presencia de valores perdidos, siempre y cuando estos estén por debajo de un límite razonable; (d) minimiza la cantidad de varianza no explicada; y (e) valora la fiabilidad y validez de los modelos de medida mediante diversos criterios.

La siguiente imagen presenta las diferencias principales entre los dos tipos de SEM:

Todos los PLS-SEM están compuestos por dos partes que forman parte del modelo, una estructural (relación entre los constructos) y otra de medida (relación entre los indicadores y los constructos que miden). Dicho de otra manera, el modelo estructural describe las relaciones entre las variables latentes (constructos) y los modelos de medida representan las relaciones entre los constructos y sus correspondientes indicadores. Respecto a este último, se deben considerar dos categorías de especificación: los modelos de medida reflectivos y formativos. En los primeros, los indicadores son los efectos o manifestaciones de un constructo subyacente; por el contrario, en los segundos, los indicadores forman el constructo por medio de combinaciones lineales.

El artículo de Ravand y Baghaei (2016) presenta de manera práctica la aplicación del PLS-SEM en R a través del paquete plspm. Los resultados de PLS-SEM se analizan siguiendo un proceso sistemático. La evaluación de la calidad de los modelos de medida y estructural se centra en estadísticos que indican la capacidad predictiva del modelo (Hair et al., 2019). De esta manera, se tienen los siguientes estadísticos de evaluación:

1. Modelos de medición reflectivos: consistencia interna (coeficiente alfa, rho_A o fiabilidad compuesta), validez convergente (cargas externas y varianza media extraía, AVE) y la validez discriminante (criterio de Fornell-Lacker o la ratio heterotrait-monotrait, HTMT).

2. Modelos de medición formativos: validez convergente (cargas externas y varianza media extraía, AVE), colinealidad entre los indicadores (factor de inflación de la varianza, VIF) y la magnitud y significación de los pesos de los indicadores.

3. Modelo de estructura: Magnitud y significancia de los coeficientes de ruta (path coefficients), coeficientes de determinación, índice de redundancia, estadísticos de bondad ajuste y relevancia predictiva.

Los PLS-SEM presentan un potencial uso en algunos campos de la psicología, por lo que, recomendamos su revisión para conocer la versatilidad de esta técnica, que tiene un uso creciente en otras áreas como las ciencias empresariales, económicas o administrativas.